УРАВНЕНИЯ ДВИЖЕНИЯ В ПРОСТРАНСТВЕ СОСТОЯНИЙ
Анализ и синтез линейных систем базируется на использовании метода пространства состояний. Сущность этого метода заключается в том, что математическая модель исследуемой системы представляется в виде системы дифференциальных уравнений в форме Коши для совокупности переменных, описывающих состояние системы и характеризующих ее поведение в будущем при условии, если известны состояние в исходный момент времени и приложенные к системе воздействия.
Уравнение собственного движения в пространстве состояний. Для получения уравнения собственного движения самолета в пространстве состояний воспользуемся системой уравнений (2.74). Тогда математическую модель можно представить следующим образом:
![]() x(t) = Ax(t)
x(t) = Ax(t)
[x(t)]T = [ДшДО Да© Ao(t) AV© ДЄ© AH(t) AL(t) х
х Дюх (I) Дюу ©Ар (I) Ду (I) Ay (I) AT (I) Az (t)] . (2.85)
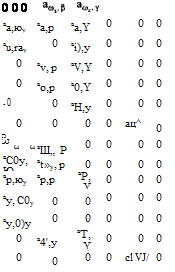
Матрица состояния полного пространственного движения самолета
 |
 |
|
А
(2.86)
Элементы матрицы А в общем случае зависят от времени A(t). Тогда уравнение состояния (2.84)-линейная нестационарная модель собственного пространственного движения самолета. Для упрощения последующих исследований будем предполагать, что элементы матрицы состояния А есть константы. Тогда уравнение (2.84) будет линейной стационарной моделью собственного пространственного движения самолета.
Решение уравнения (2.84) имеет вид
x(t) = ф(Мо) x(t0), (2.87)
где x(t0)- начальный вектор переменных состояний, определяемый при t0; t0- начальный момент времени.
Переходная матрица состояния полного пространственного движения самолета
Ф (t, t0) = I — A(t — t0) + і A2 (t — t0)2 + … = eA(t-to), (2.88)
где I-единичная матрица.
Ак tk
= Є
Тогда решением однородного уравнения (2.84), описывающего собственное движение самолета, является
x(t) = eAt х(0). (2.89)
С учетом стационарности рассматриваемой модели движения самолета выполним преобразование Лапласа для обеих частей уравнения (2.84)
где х(0)~ начальный вектор переменных состояния, определяемый при t = 0. Решение уравнения (2.90) дает
Х(р) = (Р1-А)"1 х(0). (2.91)
Вычислив обратное преобразование Лапласа от обеих частей уравнения (2.91), получим
X(t) = L-1 [(pi — А)-1] х(0), (2.92)
где L1 -оператор обратного преобразования Лапласа.
Таким образом, сравнивая (2.87) и (2.92), приходим к выводу, что переходная матрица состояния
<P(t) = L_1[(pI-А)’1], (2.93)
а ее изображение по Лапласу
Ф(р)= (pi-А);1. (2.94)
Уравнения вынужденного движения в пространстве состояний. Для
получения уравнения вынужденного движения самолета в пространстве состояний воспользуемся уравнениями (2.75)-(2.83). Тогда неоднородная математическая модель может быть представлена следующим образом:
* (I) = Ах (I) + Byuy (I) + BBuB (t). (2.95)
Векторы-столбцы входа по управляющим воздействиям и по внешним возмущениям в полном пространственном движении самолета имеют вид:
[uy(t)]T = [ASB(t) A8x(t) A6y(t) A5p(t), A53(t) A§„(t) ASz(t)] ; (2.96)
[uB(t)]T= [Afx(t)Afy(t) AmZB(t) Actw Mw(t) х
х Afz (I) Дтлв (I) Дтув (I) A0W (1) A£w (t)]. (2.97)
|
a“*A a<*A О aV.5r ЛоД 0 О о о аРА О о |
|
‘■‘cox, aw aP> aw 0 ^.O* 0 0 |
|
|||
|
|||
|
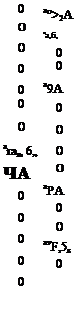 |
||
|
|||
|
|||
|
|||
|
|
||
 |
|||
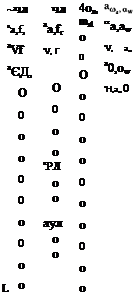 |
|||
|
|||
|
|||
|
|||
|
|||
|
|||
![]()
![]()
![]()
Элементы матриц Ву и Вв будем считать константами, а модель (2.95)-стационарной. Решение уравнения (2.95) можно представить в виде суммы общего решения (собственное движение) и частного решения (вынужденное движение): i
X (t) = Хсоб (t) + хвын (t) = Ф (t) х (0) + I Ф (t — т) Ву uy (т) dt +
о
+ 1 ф (t — т) Вв и* (т) dx. (2.100)
о
Таким образом получены уравнения собственного и вынужденного движения самолета в пространстве состояний.
